Related Rates?

So you know how a triangle has fixed values such that if you know a few, you can find the rest?  Well...in differential Calculus, you can do the same!!  If you know the rate of change of one variable, then you can find the rate of change of another related variable, usually with respect to time.  For example, if you know the rate at which helium enters a balloon, then you can also find the rate at which the radius of the balloon is expanding at different radius lenghts.  After watching the video above, I'm sure that you have the basics down, but in case you don't, let's go over them again.

 Steps:

  1. Draw a picture
  2. Label anything that's constant
  3. Identity rates of change: known and unknown
  4. Write equations with these variables
  5. Differentiate (implicitly)
  6. Plug in values and solve

Now Try this Easy Sample Problem!

Say you’re blowing up a balloon at a rate of 300 cubic inches per minute. When the balloon’s radius is 3 inches, how fast is the radius increasing?

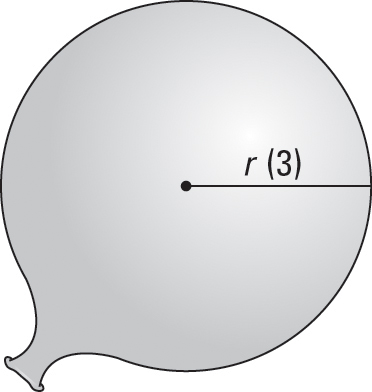
image0.jpg

  1. Label anything that's constant or is a variable

    The radius in the figure is labeled with the variable r. The radius needs a variable because, as the balloon is being blown up, the radius is changing.

    The volume of the balloon is also changing, so you need a variable for volume, V.

             There are no constants

  1. List all given rates and the rate you’re asked to determine as derivatives with respect to time.

    You’re pumping up the balloon at 300 cubic inches per minute. So

    image1.png

    You have to figure out how fast the radius is changing, so

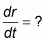
    image2.png

  2. Write down the formula that connects the variables in the problem, V and r.

    Here’s the formula for the volume of a sphere (to see more geometric formulas click here) :

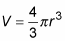
    image3.png

  3. Differentiate your formula with respect to time, t.

    image4.png

  4. Substitute known values for the rate and variables in the equation

    image5.png

    Be sure to differentiate before you plug the given information into the unknowns.

    image6.png

    So, the radius is increasing at a rate of about 2.65 inches per minute when the radius measures 3 inches.  Obviously, as we are not allowed calculators,  (300/36pi) is acceptable.

    By the way, if you plug 5 into r, rather than 3, you get an answer of about 0.95 inches per minute. By interpreting these results, we can find that the bigger the balloon gets, the slower it grows (DUH).


Don't know how to implicitly differentiate?

See the video on our home page!